Sudoku Explainedby Saul Bryan23rd July 2005 © 2005, All Rights Reserved |
|
What is Sudoku?
An example
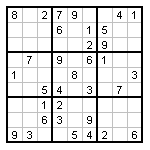
Sudoku is a number puzzle. You are given an incomplete grid, and you have to fill in all the missing values.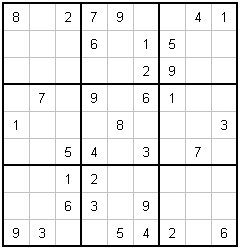 |
 |
|
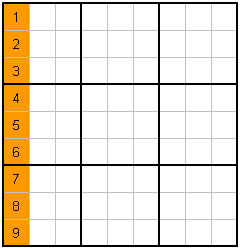
A. A typical "Easy" Puzzle |
B. The Same Puzzle, Completed. |
The Rules
The rules to Sudoku are very simple. Before I explain them though, I just want to point out that there are 3x3 blocks of 3x3 cells, each of which can hold a number from 1 to 9. Notice that the block of 3x3 cells are surrounded by a slightly thicker black border in my example.Rules : Every Row, Column and 3x3 Block contains the numbers 1 to 9
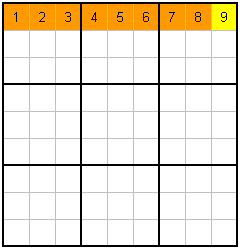
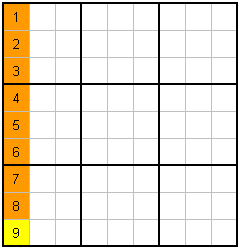
That's it! I hope you enjoyed the rules!! No seriously, that's all there is. However, I think some people respond to information more visually, so lets look at those rules again...with a little colour for emphasis.
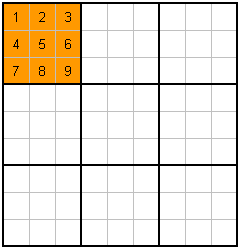 |
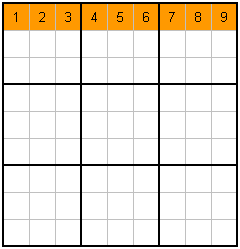 |
 |
||
C. Each Block has 1-9 |
D. Each Row has 1-9 |
E. Each Column has 1-9 |
Of course, a real puzzle has the numbers in any order, as in example B.
There is just a bit more information about the game I really think you need to know before we start working out how to actually play. They are not exactly rules, but more background information. Firstly, know that there is only ever one correct solution to each Sudoku puzzle. You can't just make them up on your own (unless you know exactly how, and it's tricky).
The next thing is, and I can't stress this enough, you can always find the correct solution from the initial given numbers without guessing. I will go further and say that you should never guess. If you find yourself saying "What if..." then you are simply guessing. Your chances of finding the right solution decrease by at least 50% each time you guess, and it's also not a satisfying way to play the game. It's also unnecessary, so please, don't do it!
Where to play the game
You may be keen to get stuck into a few games already, and I completely understand if you do. However, you may be wondering how or where you can play this game. There are sudoku puzzles popping up everywhere these days, from daily papers to paperback books filled with them. Of course, there are also countless online games to be played. You can "do a google" and find a web site that suits you, but for me, www.websudoku.com is absolutely perfect. What I like on this site is that each game is uniquely numbered, so it can be replayed easily (example A is Easy puzzle number 1,005,598,758 and yes there really are that many of them!). Printing is perfect. Data entry is easy. It has a button that lets you check you have not made any mistakes (so far). It ranks games as Easy, Medium, Hard and Evil. It also has a minimalist feel that I just like, not chock full of gnarly advertising getting you to "click me!". In fact, it reminds me of this site design quite a bit! Anyway, I strongly recommend it.How to Play the Game
Part of the fun of Sudoku is working out your own best methods of how to solve the puzzles. Although I don't think I'm spoiling the fun entirely, you may want to work this stuff out for yourself. If you think this is likely, it's best to stop reading now and start playing instead! Alternatively, you could perhaps read the "simple techniques" below just to get you started...Example Conventions
In all my examples, we are trying to deduce the value of the yellow cell with the value 9. Imagine this cell blank, and how you could work out it's value. The cells which I have coloured dark Orange are known values, such as those given to you at the start of the puzzle or other values you have discovered along the way. The examples are not complete sudoku puzzles, but simply extracts to concentrate on specific situations. You will just have to imagine other numbers being "around" these ones.Names of Techniques are just what I have decided to name them at the time. In other discussions of Sudoku, they may be called something else. I think you'll get the idea no matter what they are called. The reason why they are named at all is that in the advanced techniques you will need to use a combination of simple techniques to solve the problem. To be able to name these makes explaining these advanced techniques easier.
Simple Techniques
"Completing the Block/Row/Column"
We will start of with a technique that although simple, is unfortunately not initially all that useful. It has some use near the end of the game when the puzzle is almost finished, but is not often used at the start. The reason that I want to start here is that it's a fundamental consequence of the rules, so its dipping our toes into the waters gently and making sure you understand the rules at the same time. The idea is that if you have eight of the nine numbers in a block, row or column, then you can work out the last (missing) number. It's whatever you haven't got yet of the 1,2,3,4,5,6,7,8,9!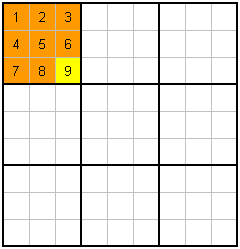 |
 |
 |
||
F. The 9 is missing and worked out |
G. The 9 is missing and worked out |
H. The 9 is missing and worked out |
If you understood the rules, this is quite an obvious thing. I'm sure you could have worked this out on your own, at least, I hope you could have. It does get more complicated from here, I promise!
"Blocking"
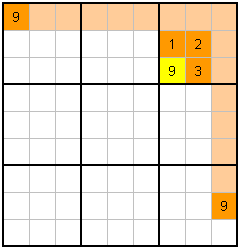
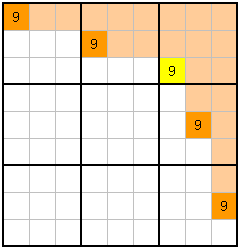
I would like to move quickly on to a much more useful technique. The idea is that you focus on a number (eg 9) in a starting block (3x3 cells, in this case, top right) and you look at the other blocks to find the same number in rows or columns. If the number is already in a row or column, you can "block it" from the starting block. To help visualize this, the "blocking" effect is highlighted in light orange in the examples below.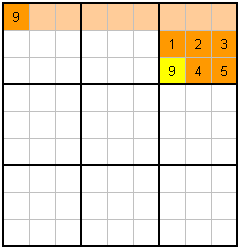 |
 |
 |
||
I. |
J. |
K. |
Have a look first at example I. This is worked out, if you like, from the rule that no column or row can have the same value more than once. So if 9 is already in that column or row, it can't be anywhere else, which extends into other blocks. The top row already has the value 9 in it, so it can't be in the blank cells in the block. As all the other cells except one have values already, this means that the nine can only go in one place as shown.
Example J is almost the same thing, but the block has less known cells. However, the column is blocked by the second 9.
Example k is fully deduced by blocking. The block with the deduced cell in it could be completely empty and we could still work out where the 9 has to go. Of course it may have some other numbers there, which you can ignore. The point is, you can work out where a number goes if the same number is in the 2 columns and 2 rows around it.
In simple Sudoku puzzles, this technique is both fast and effective. You may be forgiven into thinking that this is all you need to solve Sudoku puzzles, but it isn't. There is quite a bit more! However, it is perhaps one of the primary methods for finding values, and one of the quickest, so learn to use it.
"Counting"
This technique is a little tricker than the last, because you have to look at all numbers rather than just one. The idea is that for a particular cell, you "count" from 1 to 9 and see what values are already in use in the block/row/column that the cell belongs to. If all numbers are in use except one, then the cell must have that unused value. In more difficult puzzles, you may have two or three possible values. Even this information can be enough (in advanced techniques) to work out what some cells are.The problem with counting is that it's kinda slow. If you are trying to "beat the clock" the last thing you want to be doing is counting each cell. So, try Blocking above first, and when (or if) that stops working, start counting the most likely cells. You will get a feel for what cells are most likely to count well. Visually they will have a "variety" of numbers in the block/row/column. It's a bit hard to describe, but once you have done a few puzzles you will get an eye for this.
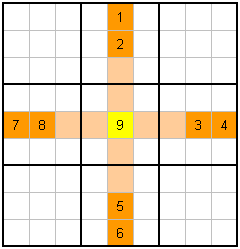
It is time for a few examples of this technique...
 |
 |
|
L. |
M. |
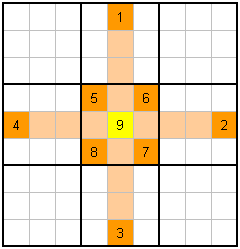
So, in example L. you can see how you can count the numbers 1 to 8 in the rows and columns for which the yellow cell belongs. This leaves only 9 unused, so it has to be the value.
Example M. uses a mixture of values known from the block, and those from the cells row/column. This is perhaps more typical a use of the technique. You will often find repeats, that is, the same value in the row, column and block. This is no big deal, it only takes one instance to count the value. Remember, what you are looking for are the missing values, as these are the possible ones for the cell. In the simple technique form, you are trying to find only one missing value.
Advanced Techniques
So far, we have covered what I consider to be the basic techniques. They work, and they work well. With blocking, counting and completing, you will be able to solve all but the harder Sudoku puzzles. In advanced techniques, you often have two (or more) steps to find the value. The intermediate steps may involve knowing what the values are, but not knowing exactly where they are. It all sounds a little airy fairy, but some examples will (I hope) clear things up.In these examples, blue cells represent empty cells where we deduce the value approximately.
Advanced Blocking
There is a trick to extend the blocking technique. This is best explained with an example...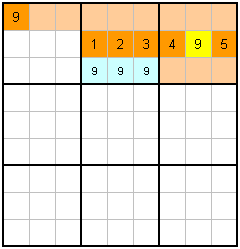 |
N. |
Take this example in two steps. Firstly, consider the middle top block. Using the Blocking technique, we know that 9 can only go on the bottom row (in blue). We don't know where exactly, it could be any of the three cells, but the important thing is that we know which row it's on. Pretend it's on that row, and use the blocking technique again, this time using the bottom row and the top row as being occupied with a 9 already. In the right top block, this narrows the place we can put the 9 into a single yellow cell, which is shown.
What's nice about this technique is that it's still fast, so it can be used at the same time as you are checking other blocking.
Advanced Counting
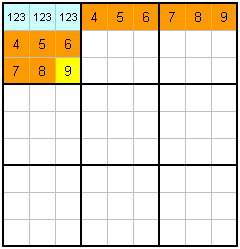
Most of the time, in harder puzzles anyway, when you count a cell you will find two or perhaps more possible values it can be. I would say if the cell has more than 4 possible values that you are counting the wrong cell, look for another one. Sometimes, if you count all cells in a row or column, you can apply further logic to the situation. As always, some examples will make sense of what I am trying to say here...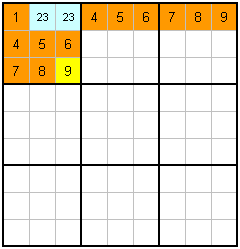 |
 |
 |
||
O. |
P. |
Q. |
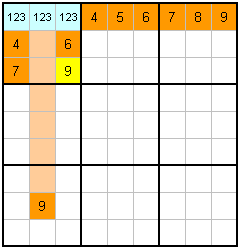
Consider example 0. The first step is to look at the top row, and realize that numbers 2 and 3 are missing from it. These can go in the blue cells, but we don't know exactly where. Then you can complete the block, counting 2 and 3 as if they were used. This leaves 9 with the unique space as marked.
Example P is the same thing, but three numbers are unknown. This is effectively the same thing.
Example Q is included to show how techniques can be mixed together sometimes. In this case, a block is included in the above logic.
You may have realized that three examples (O,P and Q) can be solved in a quicker way using blocking alone (there is a 9 on the top row). This is true, and I agree, however you may find that you have stopped looking for blocking solutions, and have turned your mind to counting techniques. Being able to recognize this situation when counting has some value.
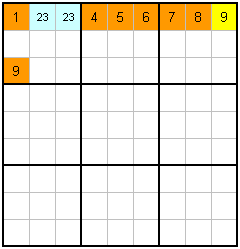 |
R. |
Example R is similar but, different! Again, you need to consider this in two steps. Firstly, use counting on the two blue cells to get the values 2,3 each. The nine in the block stops them from being 9. Then complete the top row (or count the yellow cell), counting the blue 2,3 as known even though we don't know the exact order.
Is that it?
Probably not! You may find you need even more advanced logic to solve some really seriously demented puzzles. However, I have not found one yet that I can't get out using the above techniques. Please let me know if you find one. Until then, enjoy working it out - remember it's supposed to be fun!Tutorial
Ok, it may help to go through a real Sudoku puzzle and use some of the techniques above. This is an easy puzzle, but it may not be immediately obvious how or where to even start. So let's just start at the beginning! |
S. Starting Position |
Have a quick look at the starting position. The quickest and best way to start is to look for ways to use the blocking technique. I saw one almost straight away, can you?
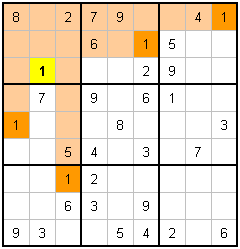 |
T. Blocking the 1 |
Ignoring all the other numbers for a moment, just look at the ones. In the top left block you can see that only one square (the yellow square) can hold the one. All the others would give you a duplicate in either the row or column, and that's against the rules (or rule, as there is only one rule really).
As this is an easy puzzle, there are quite a few more blocking numbers to find. Can you see any more? Hint : Check out the sixes in the bottom middle block.
What you will find is that when you find one number, it can sometimes be the key to finding another number, and so on. When you do manage to find a number, be sure to check to see if it has any implications for that block/row/column. In really hard puzzles, it comes down to one magic cell, which unlocks the whole thing - the trick is finding that cell!
For arguments sake, let's pretend that we can't see any more blocks, so now let's try a counting exercise. I picked a cell in the middle which looked promising...
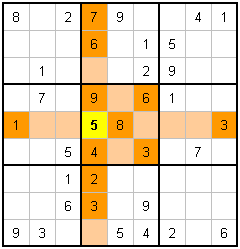 |
U. Counting the 5 |
If you focus on the Block/Row/Column that the yellow cell belongs to, and start counting from 1 to 9, you will find that all of the numbers are accounted for except for five. This is our only choice, so that's what it has to be, it's as simple as that.
Of course, other cells might give you two or more possible values. Are they a total waste? Well, no, not always as we will see in a moment. If you do count and find two or more values, it's a good idea to record them. On paper, this may be tricky as there is not a lot of space. On a computer, good programs like websudoku allow you to enter multiple values as "workings". [By the way, on Websudoku, you have to go into options to allow this]
Let's look at a slightly contrived example next of both advanced counting and completing. Concentrate on the column of the cell we just worked out...
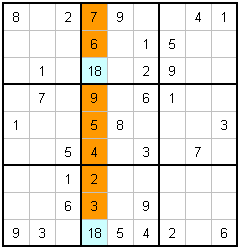 |
V. Advanced counting the column |
If you are just concentrating on the column, you can see that there are two empty cells, and these can each have a value of 1 or 8. These are shown in the blue cells above. Is this of any use? I sure you can see that it is...
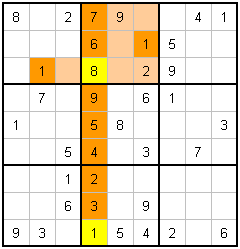 |
W. Completing the Column |
Seeing the 1 in the top blue cells row and block means that the top blue cell must be 8. This in turn, using the completing technique, means that the bottom blue cell is a 1. You get two cells solved for the price of one, bonus!!
It looks easy!
Well it might look easy, but see if you can solve it from here. You may be surprised how long it takes you. Keep in mind also that this is an easy puzzle, and they do get quite diabolically hard. The completed puzzle is at the top of this page, if you want to check you got it right!You will no doubt at some point make a mistake. There is, what I would call "false logic" where you may conclude that a cell has a certain value when in fact it doesn't have to have it. All the logic given on this page is valid, but you may be tempted, if you are adventurous, to make up your own! I am just giving you a word of warning that sometimes things sound reasonable but are not correct. Think long and hard. If you make a mistake, it may take many cells before it becomes obvious that there is a problem. You will find that there is a duplicate value in a row/column/block, and of course that's against the rules. Backtracking is difficult at that stage, so it's good to not make any mistakes in the first place! One option, while you are learning, is to use a software tool (again, like websudoku or sudokusan) that have a button to make sure you are still on the right track without actually solving the puzzle for you. Sudokusan has an automatic counter ("Initial Sweep") but I think that's a bit of a cheat. Better to do the counting yourself.
Well that's about it. I think this should provide you with enough to start off nicely into the world of Sudoku. Enjoy!
Feedback
"I gave your tips for the Sudoku puzzles to my 79 year old neighbor. With your help he was finaly able to solve a puzzle. This is great since he doesn't get out much he now has something fun to look forward to each day in the paper. Thanks for your help." - Michelle, USA."Just wanted to say thanks for the Sudoku tutorial, and thanks for mentioning Sudoku-san there. One thing I wanted to point out is that as well as the 'Initial Sweep' button (which is indeed cheating, really, but it gets people started) the Assistant has an excellent help feature, which looks at where you've got to, works out what you could do next, and explains the next step, using highlighting on the board to clarify. I think this is an excellent feature, especially for newbies, and we get a lot of feedback from people thanking us for helping them understand the more complex tricks (like x-wing, for example). Anyway, shameless self-promotion over." - Alastair
 times.
times.